In my experience a probability lesson runs smoothly about 50% of the time. Some days those pesky dice will throw sixes all afternoon, or some lucky sod will beat your thousand-to-one odds and win a fiver in the coin-toss challenge. But if you play your cards right (‘scuse the pun) these lessons can be fun for you and the students as well as a great way to challenge our in-built misconceptions about randomness and chance.
Lucky Streak: Let’s start out with my headline act. I encourage you to try this out for yourself before you read the spoiler that follows, to convince yourself it works:
Have you jotted down your fake list yet? (A string of 0s and 1s in Notepad will do). Now do the experiment for real (if you’re feeling lazy – or skint – use https://www.random.org/coins/?num=20&cur=60-gbp.1pound). Did you notice anything odd about the real coin tosses? The often surprising fact is that runs occur more frequently, and are longer, than we generally assume. This experiment works better with more coin tosses, but 20 is usually enough to see some discrepancy between an invented list and a genuine one. According to http://wizardofodds.com/image/ask-the-wizard/streaks.pdf, there is a more than 75% chance of a run of 4, and a 45% chance of a run of 5, though the actual maths involved is a bit beyond high school. Fortunately he includes a handy graph. The key idea is simple enough: a run of 5 means four coin tosses must show up the same as the previous one, which occurs with probability one in sixteen. Makes sense that you’d expect it to happen somewhere in your 20 coin tosses reasonably often. While the genuine results sometimes don’t have any striking streaks, it’s very rare for invented lists to have any more than 3 in a row before our built-in equalizer tells us we should really be balancing out the proportions. The other day I tried this with four teams for my plenary activity, and correctly identified the fake from each of the four teams. Coins, dice and roulette wheels are like Dory from Finding Nemo – getting a tail last time makes it neither more nor less likely to get one this time. We teachers know this, but are just as likely to fall into the trap of avoiding streaks as our students.
The activity described above is a nice way to get students thinking about what they understand by ‘random’. When my wife makes a patchwork quilt, a lot of time and effort goes into carefully arranging the various squares of colour to make it look random. Itunes ‘shuffle’ mode is the same – the algorithm had to be modified because true random song selection would mean you sometimes have to listen to the same song twice in a row, or three from the same artist one after the other. Once students have got it into their heads that the number 4 has a one in six chance of showing up, they expect it to show up pretty much once in every six throws. Which, for small numbers of throws, isn’t all that likely. I use this simple Excel spreadsheet to demonstrate the feebleness of small sample sizes, but also the awesome power of large ones when it comes to making predictions from a probability:
This can be modified to reflect whatever probability distribution you choose. It’s worth pointing out that there are still ‘large’ gaps numerically between the most common and least common outcomes for bigger sample sizes, but they tend to become less significant as a proportion of the whole.
Twenty wrongs makes a right:
I tried this recently with more success than I expected. Students completed the probability experiment for homework (recording the sum of two dice rolls a bunch of times), and I collated the class results in a spreadsheet. After my trick with the coin tosses they knew they wouldn’t get away with making up results, so their tables were genuine and yet not particularly close to expected values. For a sample of just 36 dice rolls each this is to be expected, but it was really interesting to show them that even their motley collection of not-too-good-looking results, when combined with each other, averaged out to resemble the theoretical distribution very closely. Again, the power of large samples coming into its own.
I use the spreadsheet above to emphasize that unlikely events not only happen, but happen with surprising predictability for a large enough sample size. How can Snickers run entire factories, employ staff and spend millions of pounds all on the off-chance that someone chooses their particular chocolate bar on a whim at the checkout? Because a tiny percentage of a large enough number is still a decent size, and while it may vary a bit, it’s actually surprisingly unlikely to fall too low. This all starts to sound like Asimov’s ‘psychohistory’, which takes the intriguing idea of predictability for large numbers to whole new levels. Nevertheless, it’s one of the most powerful ideas of probability, and I think it’s worth highlighting in between the multiplying of fractions and the drawing of tree diagrams. Incidentally, one of my self-marking homeworks is on the topic of relative frequency:
On a similar theme, I tested a theory with my year 9 class last week on the power of collective guess-work. Having just shown them how uncannily predictable their combined probability homework results were (however unpredictable each individual result may have been), I told them how the average guess for, say, the weight of a pig or the number of sweets in a jar, has been shown to be better, often, than any one person’s prediction. They clamoured for proof (in retrospect, possibly just for sweets), so I used a picture I generally reserve for trial and error lessons of a pile of bottles I once counted, and the class average guess for the number of bottles in the pile was within 1.7% of the real total! I was seriously impressed.
Randomly generate American men: I’ve included links to a few Excel files I use for probability, but it can be really helpful to be able to throw something specific together on the spur of the moment. So here’s a few Excel formulae you may find useful: =RAND() is the obvious one. Gives a random number (rectangular distribution) between 0 and 1. May equal 0 but is always less than 1. Multiply by it to scale up the range, and add to move the range. So =5*RAND()+2 gives numbers greater than or equal to 2 but less than 7. You can even round, but =RANDBETWEEN(1,6) is a simpler way to generate random integers (from 1 to 6 inclusive). Here’s a clever one for the statistics boffins among you: =NORM.INV(RAND(),0,1) gives a random number normally distributed about the mean of 0 with standard deviation 1. It uses RAND() as a probability. Use it to create realistic sample sets like heights or weights. I have it on good authority that a normal distribution with mean 178cm and standard deviation 8cm describes the heights of American men. So =NORM.INV(RAND(),178,8) will randomly generate for you an American man. Well, his height, anyway. Nifty, no? For those of you teaching A-level Statistics, the next spreadsheet combines the statistical power of Excel with the actual values provided in the tables in the AQA formula book so you can find not only the correct answers but also the answers your students should be getting. Includes binomial and normal distributions.
And if you want a nice interactive way to introduce that beautiful bell curve of the normal distribution, check out my GeoGebra version:
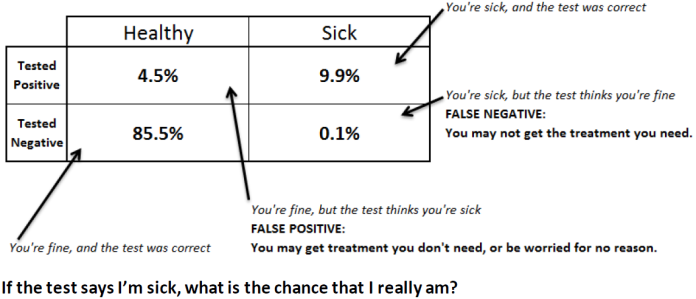
False Positive: Conditional probability is set to be a bigger part of the new GCSE, I understand. The counter-intuitive way that medical testing works makes this a really interesting example of conditional probability. The question you want to know is “Given that I tested positive, what’s the chance that I’m sick”, and it turns out the biggest factor in determining this probability is the proportion of people who get tested who are actually sick.
Random Walks: My Snail Race activity was about as fast-paced and exciting as it sounds, but at least it gave me the chance to test out a nifty method for generating random numbers on the fly. Two competitors (who are not cooperating) hold up between 1 and 4 fingers simultaneously. Add the totals together, and use the remainder when divided by 4 to determine the direction to move next (left, up, right or down). This is a nice two-dimensional way to visualise randomness (and notice how often you double-back on yourself compared to how often you might have done if you were making it up).
“I beat you, you beat him, he beats me. Wait… what?”: A probability ideas post would not be complete without at least a mention of the ingenious ‘Grime Dice’ developed by MathsGear and available here: http://mathsgear.co.uk/products/non-transitive-grime-dice . They are non-transitive, so if you memorize the order correctly this is yet another way you can reliably beat your class at an apparently fair game. Unless you memorize the order backwards, like I did. That’s a great way to reliably lose.
Er, that’s not my card: Of course, for every success there’s bound to be a probability experiment that backfires or just plain doesn’t work. Last lesson I threw 9 tails in 10 tosses while trying to demonstrate how much more likely 4, 5 or 6 was. I lost £10 to a student last year when he guessed 10 coin tosses in a row. More recently I attempted – with much skepticism, it must be said – to sway the random choice of a playing card using auto-suggestion. A subliminal poster campaign was launched a few days prior to our probability lesson, comprised of the following:
Not only did nobody think of the six of diamonds, but only two people in the whole class even had diamonds as their chosen suit. My posters must have been sub-subliminal. Sticking with the null hypothesis on this one for the time being, I reckon.