I loved maths at school. I hated learning my times tables. The beauty and underlying structure, the connections and patterns, the tricks and simplifications were all lost on me since the teaching method involved writing down every times table question from 1 to 12, in order, over and over again. Natural numbers are just that – natural. They grew inescapably from our desire to accurately describe the world around us, and their fundamental properties are also pleasingly grounded in concrete patterns and structures. By laying out objects in rectangular groupings we can not only calculate but physically experience how numbers can be separated fairly into a number of groups. Children should learn their tables, but they should develop a sense of the numbers from their inherent structure, not be required to memorize as-yet meaningless lists of facts. I want my son to be able to work out 14 times 4 as confidently as 7 times 8, and understand that it’s the same as 3.5 times 16 to boot. The structure and patterns behind numbers are more mysterious than their simple roots might suggest. Take a look at these patterns and see if you can figure out what they mean:
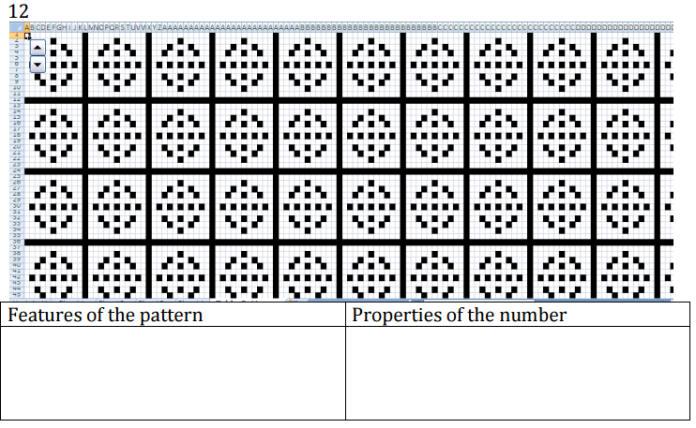
Each number forms a unique pattern. What determines the complexity and nature of the pattern? Can you deduce the rules?
Some numbers refuse to be broken down nicely into groups. They resist the urge to be separated beyond the trivial groupings of ‘all together’ or ‘all apart’. 11 sweets won’t share nicely between any group except a group of 11 or a group of 1. Most normal people might note the anomaly, perhaps try to buy 12 sweets the next time and think no more about it. Meanwhile mathematicians, in our insatiable desire to look for patterns and rules, try – and, for the most part, gloriously fail – to find an elegant explanation for the distribution of these so-called prime numbers.
The study of prime numbers, and number theory in general, is one of the most abstract areas of mathematics. Until recently, with some clever computer scientists using their very intractability to develop encryption algorithms, there was no real application anywhere in science or technology. Which makes the topic either pointless or the purest of mathematics depending on your perspective.
As a teacher, I actually hold a position that isn’t quite either of those. Primes do have specific applications to my field – I use them when making up quadratics to factorise, or fractions problems that will nicely pre-simplify, and they also enable me to do all sorts of mental maths magic on the board without pausing in my explanation (which was what impressed me most at A-level about my teachers). Here’s a few nifty things you may not have come across yet in your teaching of these topics:
Number of factors from prime decomposition: By following a straightforward branching method, any number can be separated into its unique product of primes.
From here, it is worth recognising that every factor is simply a combination, or subset, of those primes. 24 is 2 x 2 x 2 x 3, so its factors can have anything from no 2s up to all 3, and either no 3s or one 3. We can actually count the factors directly from the prime decomposition. How many 2s? (0, 1, 2 or 3) and how many 3s? (0 or 1) means 4 options followed by 2 options, giving 8 possible combinations (from no 2s and no 3s: 1, up to three 2s and one 3: 24). While primes themselves may hide their structure fiendishly well, by following this rule we can find patterns involving the number of factors for different types of number. Any number which is a power of a single prime will have one greater factors than the power (so 2 to the 6 has 7 factors). Powers of a number composed of two primes (such as 10) will have a square number of factors (10 has 4, 100 has 9, 1000 has 16, etc). Some numbers are special to us because of our number system (base 10). Count up the number of 2s and 5s in the prime factorisation of your number, and the smaller of the two numbers will give you the number of zeroes at the end of your number. Lastly, if you want an alternative explanation to why square numbers are the only ones with an odd number of factors, use the ‘product of one more than each power’ way of counting factors to see that this will only be odd if every power is even.
To investigate these patterns further, use my Factors Investigation:
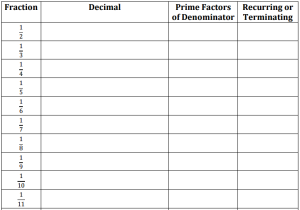
Recurring decimals: Ever wondered why fractions of powers of 2 (a half, a quarter, etc) look like powers of 5, and vice versa? As you may suspect, it comes down to the fact that 2 times 5 gives 10, the base of our number system. It’s quite an elegant way to demonstrate why some fractions give terminating expansions while others are recurring. To turn an eighth into a fraction whose denominator is a power of 10 would require multiplying top and bottom by 125, and that’s where 0.125 comes from. Have students use a calculator to identify recurring and terminating decimals for the first few numbers, then look at prime factorisations to see if they can predict which numbers will recur and which terminate:
The terminating decimals have denominators which contain no primes other than 2 or 5. Why? Base 10, of course. In base 12 we would get terminating decimals from numbers built from 2s and 3s (so a half, a third, a quarter and a sixth would be 0.6, 0.4, 0.3 and 0.2, although a fifth would now be 0.24972497… – that one took me some time!). Try this with binary and numbers that would be fine in decimal, like 0.2, become recurring (leading to floating point rounding errors, in case you’re curious how computers can sometimes get 0.1+0.2 wrong).
Modular arithmetic: I’m only just beginning to learn about this, and it’s not really that closely related to what I teach, but if you want to be able to say ‘primes are used in, er, computer security’ with a little more confidence, I recommend brushing up on your modular arithmetic and investigating public key encryption. To whet your appetite, I can convince you that the last digit of the largest known prime has to be a 1 using nothing very complicated:
I strongly recommend you carve out some time with or without your classes to investigate prime numbers some more. Here’s a spreadsheet I’ve created which lists the prime factorisation and factors of numbers, and allows you to quickly and easily examine lists of numbers. (Thanks to @colinjthomas for writing, implementing and sending me a 5-minute program to factorise the first hundred-thousand numbers all in the time it took my program to work through the first 5 thousand):

Enter any natural number up to 100,000 for its prime factor decomposition and its position relative to nearby primes.
It should be noted that recent Casio calculators have a ‘FACT’ button which allows students to find the prime factorisation of numbers directly (I don’t have this button, so I downloaded an app instead – you never know when you might need to factorise a number in a hurry…)
And lastly, if you haven’t seen datapointed.net’s visualizations of numbers I highly recommend it – a great representation of numbers in terms of their factors:






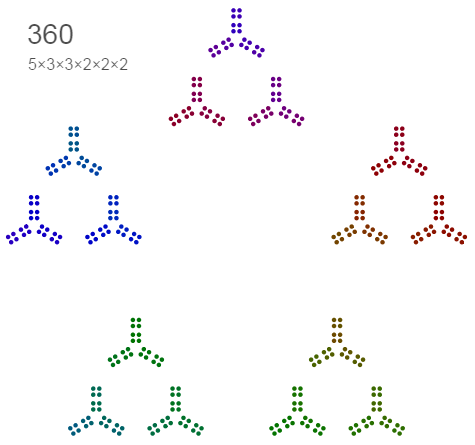
Fantastic post!
LikeLike
Thank you for the very interesting post. I didn’t get the grid patterns at first, but then I realized that they indicate the multiples of the key number in multiplication tables. It’s fun to think about patterns of little cubes in a 3d multiplication table.
I like the spreadsheet. It reminded me of a spreadsheet I made that lets you play with numbers in a prime-exponent representation. For example, 250 is represented by 1 0 3, since 250 = (2^1) * (3^0) * (5^3). This representation clarifies calculations such as fractions in simplest form and greatest common factors, and it can help us understand why sqrt(2) must be irrational. Here is the spreadsheet:
https://welltemperedspreadsheet.wordpress.com/2015/01/01/happy-0-0-1-0-0-1-0-0-0-0-1/
LikeLike
I love this idea – thanks for the link! All sorts of nice properties to operations with numbers in this form (though it may start to require commas or something for 1024, etc.
LikeLike
Thanks! I was using spaces as a delimiter, but 10-0-1 might be a clearer way to represent 5,120 than 10 0 1. Maybe a comma after every fifth prime.
LikeLike
Pingback: Prime Factor visualisations | mhorley