If you feel like your Mechanics 2 lessons are going in circles, or you don’t think you’ve got the potential to get work done, this post may be helpful to you. Remember, with great power comes great energy transfer per second.
Before I get too carried away, let me take a moment and pick up a sofa:
Moments are a great way to start the course. Straight away you’re diving into a concept they thought they had sussed (equilibrium) and saying “yeah, but if I put the two equal and opposite forces here and here, the book spins round – does that look like equilibrium to you?” We have to extend our definition to cope with rigid bodies rather than particles, but it gives scope for solving so many more problems. The sofa one I like in particular because it explains the “I’ve got the heavy end” phenomena in a way that M1 – modelling everything as particles – would miss completely. The most useful thing is that, like resolving forces in any direction you choose, you can take moments about any point and generate more information to solve a problem. Next time you’re building a cabin out of railway sleepers, take a moment and write a worksheet. Some of you may not have got round to building a cabin yet, so feel free to share a moment with me:
(This idyllic cabin beside the river where I grew up in rural Leicestershire is actually available for holidays #shamelessplug)
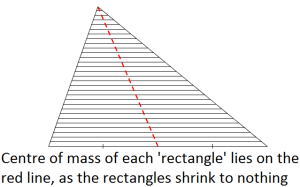
Centres of mass naturally follows on from moments, and even if the class won’t be studying volumes of revolution any time soon, it can’t hurt to throw a bit of quick calculus their way here, even if it’s just the hand-wavy kind. For instance, the centre of mass of a triangular lamina lies on each median line (from each corner to the midpoint of the opposite line). Imagine cutting the triangle into many small rectangles. The centre of mass of each is on the median, therefore so will their combined centre of mass.
I brought in a small cardboard box with a rock duct-taped to one end of the inside, and we threw it around a bit to get a feel for non-uniform objects. Remember, the centre of mass of any object can be found experimentally by suspending it from a point, balancing it on a point or even spinning it as you throw it (what this last one lacks in accuracy it makes up for in student engagement).
Energy is the first really big challenge of the course, and it should not be underestimated how confusing students can find energy questions. My booklet, All About Energy, makes for a nice introduction. Taking inspiration from BetterExplained’s ADEPT method of introducing a concept, I’ve filled the booklet with analogies, pictures and some real facts and figures (let’s face it – how many of us can find the elastic potential energy in a bungee rope but don’t know how much energy is in a bowl of Weetabix?) Best served as a full-colour, A5 booklet, it doesn’t go into great detail with the nuts and bolts, but makes a good accompaniment to your introduction:
Getting to grips with the distinctions between force, energy and power is crucial. But it’s great to be able to apply what we know about energy immediately to problems which it would be possible to solve with SUVAT equations, but by no means straight-forward:
My next example is usually a roller-coaster drawn on the board, with loop-the-loops, strange twists and turns, and definitely not constant acceleration. By knowing the height at any point (and neglecting – for now – resistance forces) the speed can be calculated easily. This will be handy later, when applying energy to circular motion. Add in friction (keep it constant for now), and the only extra information you need is the length of the track.
Energy is definitely one of those topics where I’ll need all colours of whiteboard pen available. I describe kinetic, gravitational potential and elastic potential in terms of bank accounts where we can save energy, or withdraw it. Any work done by, or against, external forces are like money being paid into the system from outside (or paid out from the system). We have no control over this energy, just like we don’t control money that isn’t ours. The difference between work done against, say, friction, and that done by weight is that we can cash in the energy we’ve ‘lost’ to work done against gravity by moving downwards to release it again. Just like money isn’t lost when I put it in an ISA in the same way that it is when I spend it in a shop.
As an improvement on SUVAT, I like to use the Felix Baumgartner example again, but this time with energy:
The bungee jump is, of course, a favourite application of elastic potential energy, but we shouldn’t ignore the humble nerf gun (easier to demonstrate in the classroom, too):
Once you get to bungee jumping, though, make sure you understand exactly what’s going on at each moment of the jump. Find a slow-motion bungee jump on youtube, or do what I did this year, and set “watch GoldenEye” as homework the lesson before:
And follow it up with a carefully researched worksheet:
As well as solutions, this worksheet includes descriptions at the end of the different phases of motion: before the rope tightens, while the rope is stretching but before maximum speed, while decelerating to rest, and the bounce back. It includes values for the energy at each point, as well as details of the forces involved. For a long time I tried to make a program that would show me exactly what was going on at any given moment during a jump, but – like many energy problems – it becomes a mean differential equation because kinetic is in terms of velocity while gravitational and elastic potential are in terms of displacement. However, I had a bit of a breakthrough and have made this little GeoGebra beauty in terms of displacement:
I like how it makes that middle section clearer: the brief time while the rope is being stretched but the force isn’t great enough to slow you down yet, only reduce your acceleration. There’s also an Excel version which will give you more precise figures, but doesn’t illustrate the concept quite so well, I think.
If you enjoyed Top Gear’s Porsche versus Beetle race, you may like to throw this activity in there at the end. It starts with SUVAT, then improves on the model using energy, assuming a constant air resistance, and then goes further by taking into account variable air resistance (don’t worry – I did the tricky maths already, so there’s a nice-ish formula for students to use). Although the last bit isn’t necessary, it makes a good extension, as this is what more and more precise mathematical modelling looks like in reality.
PS – make sure you watch the race. You know, to check your solutions:
Circular motion is the next big thing. As always, start with the definitions and spend enough time messing around with them that the formulae are not only familiar but have practically been derived by students. I like to start by asking which is going around faster; the Earth around the Sun, or the Moon around the Earth? Students will, quite correctly, come up with two different answers, depending on their interpretation, and that’s the motivation for a definition of angular speed.
Sticking with constant velocity for the moment (but that doesn’t have to be ‘horizontal circular motion’, remember), we can actually calculate the height of a geostationary orbit. That’s pretty cool, right?
Don’t be too keen to dive into ‘vertical’ circular motion. There’s so much fun to be had with the other kind:
(and, to help you out with investigating the Wall of Death further, a useful little Banked Curve Calculator in Excel.)
Finally, we’re at vertical circles. If your department doesn’t have a loop-the-loop track and a little hot-wheels car, you’ll have to build one. This is all about getting to grips with the possible scenarios. A car performing a loop-the-loop might make it all the way round without a hitch, or not quite halfway up, and roll back down, or more than halfway, and fall inwards. But what happens if the car is fixed to the track, like a roller-coaster? Or if it’s on the outside of a circular track, like driving over a bridge? While getting my head around all of this, I made a summary sheet that is as much use to me as it is to the students:
Use my GeoGebra illustration to show what happens to the forces as you go around the circle (but bear in mind the details in the previous document, as this demo is limited).
The only other thing to get your head around is that pretty much every single question will involve forces and energy. Resolve towards the centre, because you know that will be equal to the centripetal force which we have a formula for. And use conservation of energy, combined with the height, to find the speed. The link here is the speed.
And today’s homework is to watch Fifth Gear make loop-the-loop work in reality:
And, of course, answer questions on it:
The final chapters of M2 take us beyond SUVAT at last. The progression began back at GCSE (or earlier) with the constant speed equation, was developed further into the constant acceleration equations in M1, and now, in quick succession, using calculus to describe motion when acceleration is given as a function of time, then using differential equations to describe motion when acceleration is a function of displacement. This opens the doors wide on all sorts of problems, and even though many of them can only be solved using much more advanced techniques, being able to generate the formulae is half the battle in the days of WolframAlpha which will solve your differential equations for you.
The nicest application of these topics, though, brings us right back to circular motion. It is useful for a teacher to be able to derive the formulae for centripetal acceleration for constant angular velocity. It’s worth being aware of the derivation for variable angular velocity also, but probably not worth the half-hour it would take to go through it in class!
As with M1, I’ve made a Checklist; those key skills which are potential limiting factors for success in M2, but do not, on their own, constitute a full understanding of the module.
The M2 Ideas Test, on the other hand, is often a considerable challenge even for A-grade students, and will really test how comprehensive and thorough a student’s understanding truly is.
And, of course, the M2 Not-Formula Book and the one-page M2 Essentials revision card, both of which summarise key information from the course which will not be provided in the formula booklet, and are highly recommended for independent revision and reinforcement of ideas.
I’d love to hear your thoughts on any of these resources, and of course any others you have found particularly useful.